Chapter 1: Understanding the Concept of i^i

What exactly is i^i and what does it signify? The answer may astonish you!

We start by defining the imaginary unit i as the square root of -1. This concept might seem perplexing, especially since we were taught in school that negative numbers cannot have square roots. However, this misconception is not entirely accurate. If you're intrigued, consider the following peculiar result: if you input i^i into a calculator equipped with the imaginary unit, the output will be the real number approximately equal to 0.20787957635... Yes, a real number indeed!

Let’s delve deeper into this intriguing topic.

In the 18th century, the brilliant mathematician Leonhard Euler explored the square roots of negative numbers—a concept that was quite unconventional at the time. He made a remarkable discovery: i^i is, in fact, a real number. Specifically, he found that:

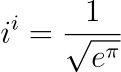
When you input this expression into a calculator, it yields the same result of approximately 0.20787957635. You can verify this with tools like Wolfram|Alpha.

What’s going on here? Is i^i genuinely a real number?

To comprehend an expression like i^i, we must first clarify our definitions, which can be quite ambiguous. This is analogous to stating that the square root of 4 is 2; while this is true, -2 is also a valid square root of 4, as it satisfies the equation x² = 4. Thus, we need to specify which “side” of zero we are on the real number line, indicating that there are indeed two square roots of 4. This is similar to what occurs in the complex plane.

Remember, a complex number can be represented as a point in a two-dimensional plane, where the real number a is represented by the point (a, 0) and bi by the point (0, b). This concept is not arbitrary; complex numbers can be treated as a vector space over the reals, incorporating additional multiplicative structures consistent with real numbers. Consequently, we can express the complex number (a, b) as a + bi.

To multiply two complex numbers, we expand the brackets and apply the rule i² = -1. For instance, we can verify that (a + bi)(c + di) = ac - bd + (ad + bc)i.

Now, let's reproduce Euler’s astonishing result by utilizing a classical theorem. Every complex number a + bi, characterized by its modulus (distance from the origin) r and argument (angle to the real axis), can be expressed in polar form as:

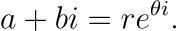
Here, e represents Euler’s famous constant, approximately equal to 2.7182818... This follows from Euler's remarkable formula:

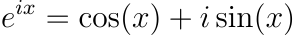
With i being the unique complex number with modulus r = 1 and argument θ = π/2, we can express i as:

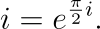
By raising both sides of this equation to the power of i, we obtain:

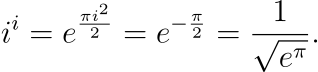
However, we need to tread carefully with this calculation. By applying Euler’s formula, we notice that the exponential function is periodic with a period of 2πi. This is an extraordinary insight, beautifully linking trigonometry and calculus.

Because of this periodicity, we arrive at:

for all integer values of k. Now, let's extract i^i from this broader expression. We can derive:

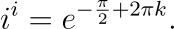
where k can be any integer.

It’s important to note that the sign in front of 2πk can be either positive or negative, as k can represent any integer. This leads us to a multivalued expression that is technically complex but can be viewed in a way that reflects the nature of the function f(x) = x^i, which yields infinitely many values for each input x.

Alternatively, we can define the process of raising a number to a complex power by selecting a so-called branch cut, ensuring that we can discuss holomorphicity (complex differentiability). This involves deciding which 'equivalent' angles we use to represent complex numbers. If we opt for what is known as the principal branch, we arrive at Euler’s curious result; however, other branches are equally valid.

Ultimately, it is fascinating to note that regardless of how we define the operation of exponentiating by a complex number, any representative value of i^i is a real number, and all corresponding values (depending on k) hold true in each definition.

I perceive this "number" as comprising infinitely many values (along the real line), akin to how I view the nth roots of a number as n vertices of a regular n-gon inscribed in a circle.

This phenomenon is one of the many enigmas in mathematics that can be challenging to grasp, and it often requires some adjustment to accept.

As John Von Neumann once remarked to Felix Smith, "Young man, in mathematics you don’t understand things. You just get used to them." While I don’t fully endorse this statement in every context, it rings true in this instance; we must simply accept this complexity.

Upon reflection, this multivalued nature is not dissimilar to the situation encountered when finding antiderivatives of a function. No single function can claim to be the sole true antiderivative, as there are infinitely many antiderivatives associated with a given function.

In a way, Euler discovered the most natural representation of i^i, correlating it to the representation of the real integral ∫ 1/x dx as ln(x). However, all expressions of the form ln(x) + C are valid antiderivatives of 1/x for any real number C, even though C = 0 may seem the most intuitive case.

Regardless, the fact that all representations of i^i yield real numbers remains an astonishing aspect of mathematics.

Thank you for reading!

If you enjoy articles like this, consider joining Medium for full access to the community. Simply click here.

Chapter 2: Exploring the Unusual Appearances of Pi

In this section, we will delve into the unusual ways that Pi manifests itself in mathematics.

The first video titled "The Most Unusual Ways Pi Shows Up In Mathematics | Can You Explain These?" offers fascinating insights into the unexpected appearances of Pi in various mathematical contexts.

Chapter 3: Analyzing the Fundamental Flaws in Mathematics

Now, let’s shift our focus to the fundamental flaws found in mathematics.

The second video titled "Math's Fundamental Flaw" presents a critical examination of the underlying issues within the mathematical framework.